读一下这篇Survey，顺便做点阅读笔记，先从Introduction后的第一部分Problem Setting And Terminology开始：
一些术语与定义
-
LR - Low-resolution；
-
HR - High-resolution；
-
SR - Super-resolution 简单的理解即是将图像通过一定的技术处理，从低分辨率（LR）还原到高分辨率（HR）的过程；
LR图像被定义为HR图像经降采样后得到的输出，最常见的降采样操作是带上抗锯齿参数的双立方插值，也有更复杂效果更优的方法：
$$\mathcal{D}\left(I_{y} ; \delta\right)=\left(I_{y} \otimes \kappa\right) \downarrow_{s}+n_{\varsigma},{\kappa, s, \varsigma} \subset \delta$$
即将图像$I{_y}$与Blur Kernel $k$卷积后加上一定的高斯白噪音$n_{\varsigma}$。
图像质量评价指标
1. 峰值信噪比 - PSNR
先定义MSE（均方误差）为：
$$M S E=\frac{1}{m n} \sum_{0}^{m-1} \sum_{0}^{n-1}\|f(i, j)-g(i, j)\|^{2}$$
再做一些数学处理，即可得到PSNR：
$$PSNR=20 \log _{10}\left(\frac{M A X_{f}}{\sqrt{M S E}}\right)$$
其中图像尺寸为$m\times n$，$f$表示原HR图像，$g$表示经过SR处理的重建图像，$MAX{_f}$表示图片的最大像素值，当每个采样值有$n$个bit的时候，有：
$$MAX{_f}=2^n-1$$
通常情况下 $n=8$，则$MAX{_f}=255$。
由公式可见，MSE其实就是原图像与重建图像在每个像素上的误差之平方的平均值；而PSNR则是将$MAX{_f}^2$与MSE相比再取对数，其单位为db，越大说明原图像与重建图像越相似。 然而由于PSNR只关注像素层面的对应而非整体视觉效果，其评价结果不一定符合人类对SR的期望。但它仍然是运用得最广泛的评价指标之一。
2.结构相似性 - SSIM
由于人类视觉系统（HVS）更加看重图像的整体结构信息，有人基于此提出了一种符合人类直觉的评价方法 - SSIM。
SSIM的计算依赖以下值：亮度 - luminance、对比度 - contrast、 结构 - stuctures，其计算流程在原论文中以下图展示，做得非常明了：
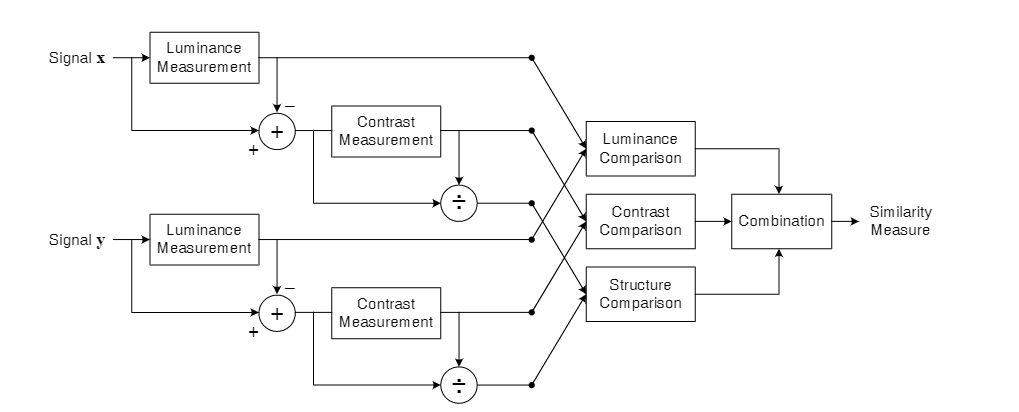对原图像$I$、重建图像$\hat{I}$：
对于亮度，求其像素强度的均值$\mu{_I}$、$\mu{_\hat{I}}$：
$$\mu_{I}=\frac{1}{N} \sum_{i=1}^{N} I(i)$$
对于对比度，求标准差$\sigma{_I}$、$\sigma{_\hat{I}}$：
$$\sigma_{I}=\left(\frac{1}{N-1} \sum_{i=1}^{N}\left(I(i)-\mu_{I}\right)^{2}\right)^{\frac{1}{2}}$$
对于结构，求$I$与$\hat{I}$的协方差$\sigma_{I \hat{I}}$：
$$\sigma_{I \hat{I}}=\frac{1}{N-1} \sum_{i=1}^{N}\left(I(i)-\mu_{I}\right)\left(\hat{I}(i)-\mu_{\hat{I}}\right)$$
其中的$I(i)$即表示第$i$个像素的强度。
则可得亮度差异：
$$\mathcal{C}_{l}(I, \hat{I})=\frac{2 \mu_{I} \mu_{\hat{I}}+C_{1}}{\mu_{I}^{2}+\mu_{\hat{I}}^{2}+C_{1}}$$
对比度差异：
$$\mathcal{C}_{c}(I, \hat{I})=\frac{2 \sigma_{I} \sigma_{\hat{I}}+C_{2}}{\sigma_{I}^{2}+\sigma_{\hat{I}}^{2}+C_{2}}$$
以及结构差异：
$$\mathcal{C}_{s}(I, \hat{I})=\frac{\sigma_{I \hat{I}}+C_{3}}{\sigma_{I} \sigma_{\hat{I}}+C_{3}}$$
其中$C_{1}=\left(k_{1}\times MAX{_f}\right)^{2}$与$C_{2}=\left(k_{2}\times MAX{_f}\right)^{2}$是为避免除零而添加的常数，有$k_{1} \ll 1$和$k_{2} \ll 1$，一般地，分别取作$0.01$与$0.03$；$C{_3}$同理，常取$C{_3}=C{_2}/2$。 最后得：
$$\operatorname{SSIM}(I, \hat{I})=\left[\mathcal{C}_{l}(I, \hat{I})\right]^{\alpha}\left[\mathcal{C}_{c}(I, \hat{I})\right]^{\beta}\left[\mathcal{C}_{s}(I, \hat{I})\right]^{\gamma}$$
式中$\alpha,\beta,\gamma $为调整权重用的参数，常取$\alpha=\beta=\gamma=1 $。在实际计算中常取多个小块滑动计算后再取平均值得到全图SSIM。 $SSIM\in [-1,1]$，其越接近1时说明$I$与$\hat{I}$越相似。
3.平均主观得分 - MOS
顾名思义，请受试者对重建图像进行主观打分（常为1-5分）后取平均值。
4.Learning-based Perceptual Quality
使用机器学习的方法训练模型进行评价。
5.基于任务效果进行评估 - Task-based Evaluation
将SR的结果投入到其他的实际任务中去，观察其效果以评价图像。